Klein, comme Etienne ?!
Et bien non.
La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925).

L’appellation « bouteille » proviendrait d’une erreur d’un traducteur qui aurait confondu en allemand « kleinsche Fläche » (surface de Klein) et « kleinsche Flasche » (bouteille de Klein), et désigné en anglais cette surface par « Klein bottle ».
Autres noms : surface de Klein, tore de Klein, tore non orientable.
Un tore, c’est un un objet mathématique en forme de donut, nous garderons donc « bouteille ».

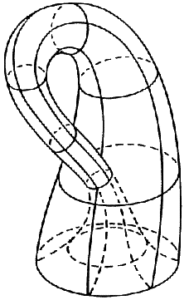
L’intersection de la bouteille avec elle-même n’existe que sur cette projection en trois dimensions.

Cette bouteille de Klein qui n’existe que pour les mathématiciens est une surface fermée, sans bord et non orientable, c’est-à-dire une surface pour laquelle on ne peut pas définir un « intérieur » et un « extérieur ».
En fait, une bouteille de Klein, c’est juste une surface sans bord semblant délimiter un volume qui n’a pas d’intérieur…
C’est un exemple relativement simple de surface qu’on ne peut pas convenablement dessiner dans l’espace en trois dimensions : cet objet mathématique n’existe que dans un espace à quatre dimensions, et toute représentation en trois dimensions est incorrecte.

Si la représentation classique ressemble bien à une bouteille (que l’on n’arriverait jamais à remplir de liquide !), n’importe quelle surface engendrée par le mouvement d’un cercle (de rayon variable ou non) ou même d’une courbe fermée qui revient sur elle-même après rotation d’un demi-tour est une représentation de la bouteille de Klein, à condition de ne pas oublier de faire ce mouvement dans un espace à quatre dimension.

Pour simplifier (?) on pourrait dire que la bouteille de Klein serait un ruban de Möbius gonflé dans un espace à quatre dimensions. Ou que la bouteille de Klein est au tore (ou : donut, souvenez-vous) ce que l’anneau de Möbius est au ruban.
L’anneau de Möbius, comme on sait, est ce ruban sur lequel une fourmi qui marche toujours dans la même direction est certaine de repasser par son point de départ, tel les Dupont-Dupond. Et elle aura alors arpenté les deux faces du ruban.

Mais si elle part dans la mauvaise direction, elle va tomber dans le vide, car le ruban a un bord (apparemment deux, à droite et à gauche de la fourmi, mais si on regarde bien c’est le même).
Le donut-tore, lui, n’a pas de bord. On peut marcher indéfiniment dessus, dans n’importe quelle direction, on ne tombera pas. Mais à moins de faire un trou à sa surface on ne peut pénétrer à l’intérieur : on peut lécher le sucre glace du donut mais il faut mordre et creuser pour savoir s’il est fourré à la confiture ou au chocolat. La surface de Klein (et donc la bouteille) est comme un donut dans lequel mordre ne sert à rien : il n’y a pas d’intérieur, et cela se voit… de l’extérieur.
Une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius, c’est-à-dire deux surfaces qui n’ont qu’un seul bord ! (alors que la bouteille de Klein, elle, n’en a aucun, rappelez-vous… contradiction apparente qui ne doit pas vous surprendre : une noix n’a pas de bord, ouverte elle offre deux coquilles de noix avec chacune son plat-bord).
Si l’on voulait faire une bouteille de Klein en papier, il suffirait donc de coudre deux anneaux de Möbius le long de leur côté et de souffler au milieu… (vous pouvez toujours tenter !)

Quelles sont ces choses étranges dont nous parlent les mathématiciens ? Faut-il toujours des fourmis marcheuses pour les décrire ? Et d’ailleurs ne nous parlent-ils que de choses étranges ? Ces choses sont-elles toutes des « objets mathématiques » ?
Facilement fasciné par des formes impossibles, n’oublirions-nous pas que la droite d’Euclide, qui ne commence ni ne finit et n’a pas d’épaisseur, est un objet tout aussi extraordinaire ?
Finalement, Klein a-t-il découvert, fabriqué, inventé sa bouteille ou l’a-t-il simplement décrite comme un entomologiste ?
Les mathématiciens découvrent-ils des objets ici et là, ou les créent-ils ?